2020. 11. 25. 11:42ㆍ코딩테스트 준비/python
그리디 알고리즘
- 그리디 알고리즘(탐욕법)은 현재 상황에서 지금 당장 좋은 것만 고르는 방법을 의미
- 일반적인 그리디 알고리즘은 문제를 풀기 위한 최소한의 아이디어를 떠올릴 수 있는 능력을 요구합니다.
- 정당성 분석이 중요
<문제> 거스름 돈: 문제 설명

- 최적의 해를 빠르게 구하기 위해서는 가장 큰 화폐 단위부터 돈을 거슬러 주면 된다.

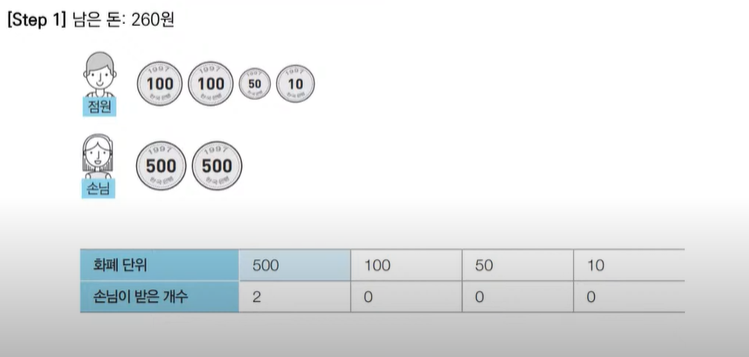


<문제> 거스름 돈: 정당성 분석
- 가장 큰 화폐 단위부터 돈을 거슬러 주는 것이 최적의 해를 보장하는 이유는?
- 가지고 있는 동전 중에서 큰 단위가 항상 작은 단위의 배수이므로 작은 단위의 동전들을 종합해 다른 해가 나올 수 없기 때문입니다.
<문제> 거스름 돈: 답안 예시(Python)
n = 1260
count = 0
# 큰 단위의 화폐부터 차례대로 확인하기
array = [500, 100, 50, 10]
for coin in array:
count += n // coin # 해당 화폐로 거슬러 줄 수 있는 동전의 개수 세기
n %= coin
print(count)
<문제> 거스름 돈: 시간 복잡도 분석
- 화폐의 종류가 K라고 할 때, 소스코드의 시간 복잡도는 O(K)입니다.
<문제> 1이 될 때까지: 문제 설명
- 어떠한 수 N이 1이 될 때까지 다음의 두 과정 중 하나를 반복적으로 선택하여 수행하려고 합니다. 단, 두번째 연산은 N이 K로 나누어 떨어질 때만 선택할 수 있습니다.
1. N에서 1을 뺍니다.
2. N을 K로 나눕니다.
- 예를 들어 N이 17, K가 4라고 가정합시다. 이때 1번의 과정을 한 번 수행하면 N은 16이 됩니다. 이후에 2번의 과정을 두 번 수행하면 N은 1이됩니다. 결과적으로 이 경우 전체 과정을 실행한 횟수는 3이 됩니다. 이는 N을 1로 만드는 최소 횟수입니다.
- N과 K가 주어질 때 N이 1이 될 때까지 1번 혹은 2번의 과정을 수행해야 하는 최소 횟수를 구하는 프로그램을 작성하세요.
<문제> 1이 될 때까지: 문제 조건
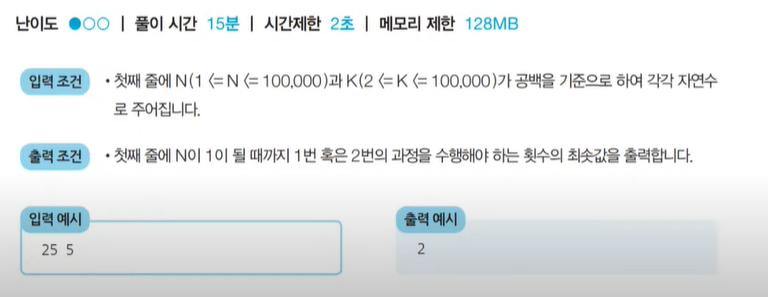
<문제> 1이 될 때까지: 문제 해결 아이디어
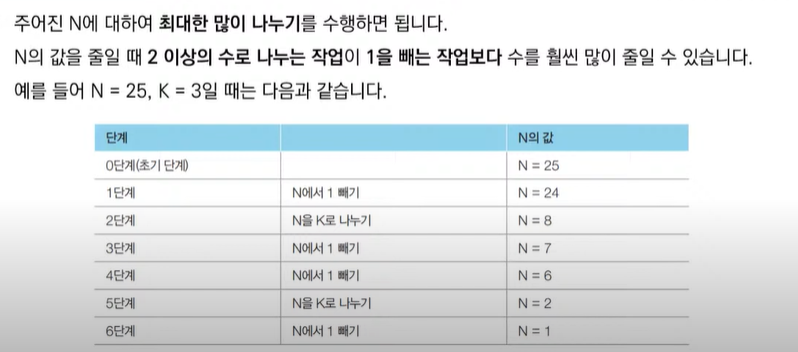
<문제> 1이 될 때까지: 정당성 분석
- 가능하면 최대한 많이 나누는 작업이 최적의 해를 항상 보장할 수 있을까요?
- N이 아무리 큰 수여도, K로 계속 나눈다면 기하급수적으로 빠르게 줄일 수 있습니다.
<문제> 1이 될 때까지: 답안 예시 (Python)
# N, K을 공백을 기준으로 구분하여 입력 받기
n, k = map(int, input().split())
result = 0
while True:
# N이 K로 나누어 떨어지는 수가 될 때까지만 1씩 빼기
target = (n // k) + k
result += (n - target)
n = target
# N이 K보다 작을 때 (더 이상 나눌 수 없을 때) 반복문 탈출
if n < k:
break
# K로 나누기
result += 1
n //= k
# 마지막으로 남은 수에 대하여 1씩 빼기
result += (n - 1)
print(result)
<문제> 곱하기 혹은 더하기: 문제 설명
- 각 자리가 숫자(0부터 9)로만 이루어진 문자열 S가 주어졌을 때, 왼쪽부터 오른쪽으로 하나씩 모든 숫자를 확인하며 숫자 사이에 'x' 혹은 '+' 연산자를 넣어 결과적으로 만들어질 수 있는 가장 큰 수를 구하는 프로그램을 작성하세요. 단, +보다 x 를 먼저 계산하는 일반적은 방식과는 달리, 모든 연산은 왼쪽부터 순서대로 이루어진다고 가정합니다.
<문제> 곱하기 혹은 더하기: 문제 조건
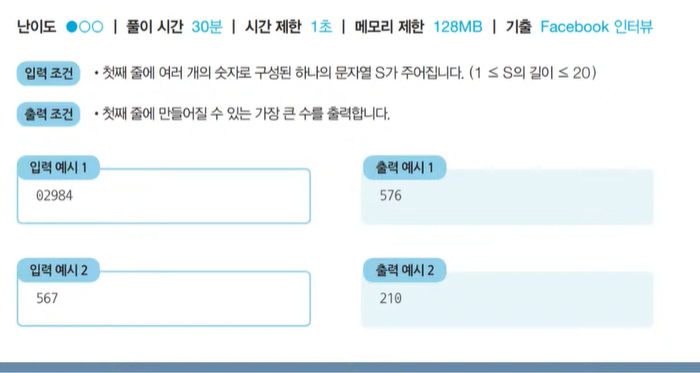
<문제> 곱하기 혹은 더하기: 문제 해결 아이디어
- 대부분의 경우 '+'보다는 'x'가 더 값을 크게 만듭니다.
- 예를 들어 5 + 6 = 11이고, 5 x 6 = 30입니다.
- 다만 두 수 중에서 하나라도 '0' 혹은 '1'인 경우, 곱하기보다는 더하기를 수행하는 것이 효율적입니다.
- 따라서 두 수에 대하여 연산을 수행할 때, 두 수 중에서 하나로 1 이하인 경우에는 더하며, 두 수가 모두 2 이상인 경우에만 곱하면 정답입니다.
<문제> 곱하기 혹은 더하기: 답안 예시 (Python)
data = input()
# 첫 번째 문자를 숫자로 변경하여 대입
result = int(data[0])
for i in range(1, len(data)):
# 두 수 중에서 하나라도 '0' 혹은 '1'인 경우, 곱하기보다는 더하기 수행
num = int(data[i])
if num <= 1 or result <= 1:
result += num
else:
result *= num
print(result)